
The time T m at which y is maximum is at the vertex of y = y 0 + V 0 sin(θ) t - (1/2) g t 2 and is given by
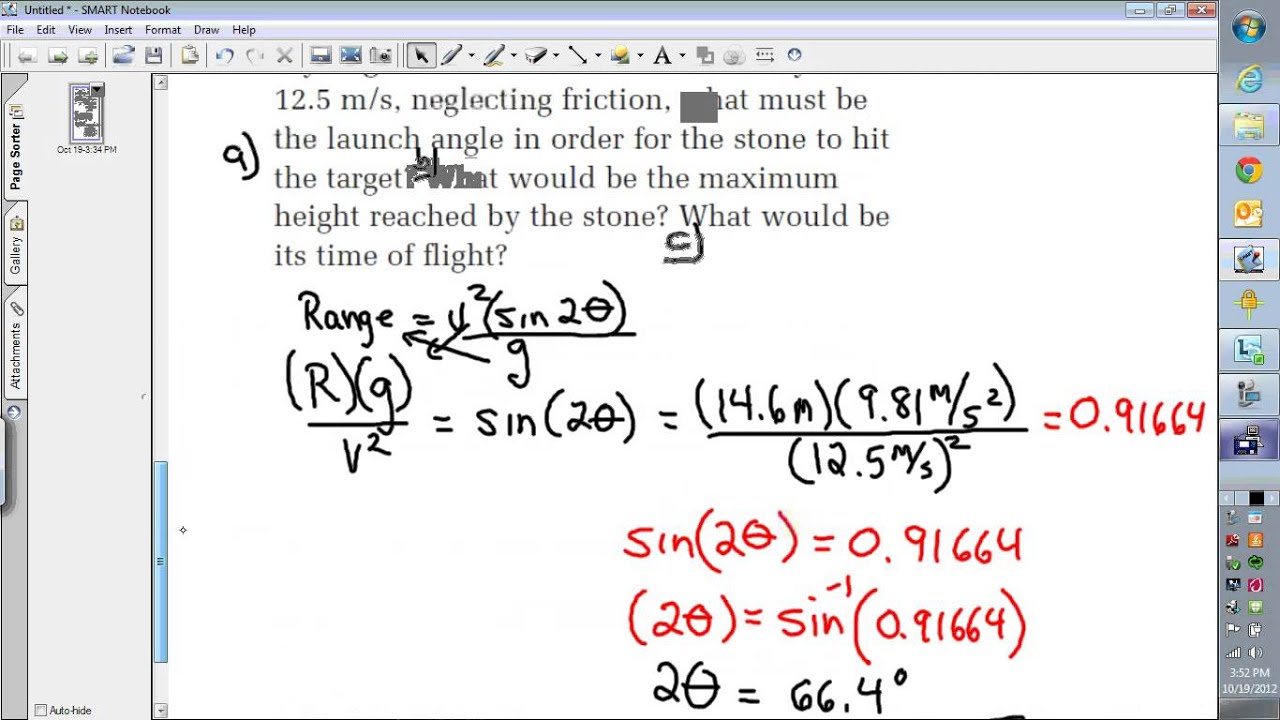
The displacement is a vector with the components x and y given by: V x = V 0 cos(θ) and V y = V 0 sin(θ) - g t The vector acceleration A has two components A x and A y given by: (acceleration along the y axis only)Īt time t, the velocity has two components given by The vector initial velocity has two components: V 0x and V 0y given by: Projectile Equations used in the Calculator and Solver Range = 50m, Initial Velocity: V 0 = 30m/s, Initial Height: y 0 = 10mĭecimal Places = 4 Initial Angle = ° Maximum Height = meters Flight Time= seconds Equation of the Path:: y = x 2 + x + The outputs are the initial angle needed to produce the range desired, the maximum height, the time of flight, the range and the equation of the path of the form \( y = A x^2 + B x + C\) given V 0 and y 0. Initial Velocity: V 0 = 30m/s, Initial Angle: θ = 50°, Initial Height: y 0 = 10mĭecimal Places = 4 Maximum Height = meters Flight Time= seconds Range = meters Equation of the Path: y = x 2 + x +Ģ - Projectile Motion Calculator and Solver Given Range, Initial Velocity, and Height Enter the range in meters, the initial velocity V 0 in meters per second and the initial height y 0 in meters as positive real numbers and press "Calculate". The outputs are the maximum height, the time of flight, the range and the equation of the path of the form \( y = A x^2 + B x + C\). The projectile equations and parameters used in this calculator are decribed below.ġ - Projectile Motion Calculator and Solver Given Initial Velocity, Angle and Height Enter the initial velocity V 0 in meters per second (m/s), the initial andgle θ in degrees and the initial height y 0 in meters (m) as positive real numbers and press "Calculate".

An online calculator to calculate the maximum height, range, time of flight, initial angle and the path of a projectile.


 0 kommentar(er)
0 kommentar(er)
